![]()
![]()
![]()
Next: Introduction
Partitioned Steiner 5-Designs
Reinhard Laue, Alfred Wassermann,
University of Bayreuth, Germany
Abstract:
Orbits of 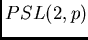 on 6-element subsets of the projective line with
prescribed non-trivial stabilizer are described. A refinement of cross-ratio
computations to
on 6-element subsets of the projective line with
prescribed non-trivial stabilizer are described. A refinement of cross-ratio
computations to 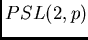 orbits allows to determine the orbits on
5-element subsets that they cover. Then Steiner
orbits allows to determine the orbits on
5-element subsets that they cover. Then Steiner 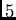 -
-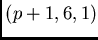 designs
are assembled from them. In particular, there is one isomorphism type
of
designs
are assembled from them. In particular, there is one isomorphism type
of 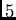 -
-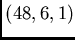 designs that consists of
designs that consists of 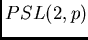 orbits of the same size,
each being a
orbits of the same size,
each being a 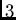 -
-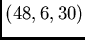 design. There are 7 isomorphism types
of
design. There are 7 isomorphism types
of 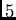 -
-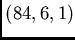 designs of this type. Generally, Steiner
designs of this type. Generally, Steiner 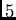 -
-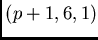 designs
with such an orbit partition may only exist if
designs
with such an orbit partition may only exist if
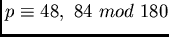 .
.
- Introduction
- Basic Conditions
- Subgroups of order up to 6 in
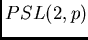
- Invariants
- Bibliography
- About this document ...
N.N. 2002-02-25