´

next up previous
Next: Subgroups of order up Up: Partitioned Steiner 5-Designs Previous: Introduction

Basic Conditions

In this section we investigate some necessary conditions that have to hold if there exists a $5$-$(p+1,6,1)$ design with automorphism group . So we throughout assume $V$ to be a point set of $v = p+1$ points. A $n$-set simply means a subset of size $n$ of $V$.


We start using only some divisibility conditions.


Theorem 1: If $5$-$(v,6,1)$ is an admissible parameter set for a $t$-design then $v$ is even. If in addition $v = p+1$ for some prime $p$ then 3 divides $p+1$ and 5 does not divide $p+1$.

Proof By double counting the number $b$ of blocks of a $t$-$(v,k,\lambda)$ design is always

\begin{displaymath} b = \lambda_t {v \choose t}/{k \choose t} \end{displaymath}

where $\lambda_t = \lambda$.

Because a $t$-design is also a $(t-1)$-design with the same number of blocks the corresponding formula for $t-1$ yields the $\lambda_{t-1}$. In case $k = 6$ and $t = 5$ then $\lambda_{t-1} = (v-4)/2$ such that $v = p+1$ is even.

Continuing with $t-2$ in the same way then $\lambda_{t-2} = (v-3)(v-4)/6$ such that if $p \ne 3$ then 3 does not divide $v-4$ and hence has to divide $v = p+1.$ The case $p = 3$ is clearly impossible.

Continuing in this way we obtain from the formula for $\lambda_1$ that 5 is a divisor of $(v-1)(v-2)(v-3)(v-4)$ such that 5 does not divide $p+1$. $\Diamond$


We get some sharper results if we assume as a group of automorphisms. Our main tool will be to analyse orbits of on subsets $S$ of the point set $V$ by looking at the set stabilizer of such a subset.


We introduce some general notations. We assume that a finite group $G$ acts on a finite set $V$ of $v$ points. For a subset $S$ of $V$ the length of the orbit $S^G$ under $G$ is

\begin{displaymath}\vert S^G\vert \ = \ \frac{\vert G\vert}{\vert N_G(S)\vert}.\end{displaymath}

Orbits on $t$-sets $T$ and $k$-sets $K$ for $t \le k$ are related by some numbers which are important for the construction of $t$-designs.


We define

\begin{displaymath}\lambda(T,K^G) \ = \ \vert\{K'\vert T\subset K'\in K^G\}\vert\end{displaymath}

and

\begin{displaymath}\mu(T^G,K) \ = \ \vert\{T'\vert T'\subset K, T'\in T^G\}\vert.\end{displaymath}

Then we obtain a general formula already used by Alltop in 1965, [1].


Alltop's Lemma 2: Let a group $G$ act on a set $V$ and let $T\subset V$ be a $t$-set and $K\subset V$ a $k$-set of $V$. Then

\begin{displaymath}\vert T^G\vert \lambda(T,K^G) = \vert K^G\vert \mu(T^G,K)\vert.\end{displaymath}


This follows easily by doubly counting

\begin{displaymath} \vert\{(S,B)\vert S \in T^G, B \in K^G, S\subset B\}\vert. \end{displaymath}

$\Diamond$

The group $G$ acts $t$-homogeneously if it is transitive on the $t$-sets.

Corollary 3: Let $G$ act $t$-homogeneously in Alltop's Lemma. Then

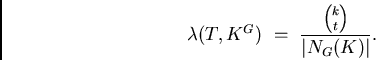
\begin{displaymath}\lambda(T,K^G) \ = \ \frac{{k\choose t}}{\vert N_G(K)\vert}.\end{displaymath}


Proof. Substituting $\mu(T^G,K) = {k\choose t}$, $\vert T^G\vert = \frac{\vert G\vert}{\vert N_G(T)\vert}$, and $\vert K^G\vert = \frac{\vert G\vert}{\vert N_G(K)\vert}$ in the equation and cancelling $ \vert G\vert$ yields the claimed result. $\Diamond$


In the special case of and $t = 3,\ k = 5$ we obtain that divides 10. In particular, if 5 does not divide this implies that divides 2.


We will construct orbit representatives by constructing $k$-sets invariant under a prescribed subgroup $U$. From these we first have to remove those invariant under a larger group and then have to decide whether they lie in the same orbit. This can be done using the next Lemma [15].


Lemma 4 Let a group $G$ act on a set $V$ and let $T_1, \ T_2 \subset V$ be two t-sets having the same stabilizer $U$ in $G$. Let $T_1 ^g = T_2$ for some $g \in G$. Then $g \in N_G(U)$.


Proof. We have

\begin{displaymath}U^g = N_G(T_1)^g = N_G(T_1^g) = N_G(T_2) = U\end{displaymath}

such that $g \in N_G(U)$. $\Diamond$


If 5 divides then 5 divides $p-1$ by Theorem 1. We know from group theory [10] that then there exists only one conjugacy class of subgroups of order $p-1$ in . Such a subgroup is a dihedral group $D$ with a cyclic normal subgroup of order $\frac{p-1}{2}$. A subgroup $U$ of order 5 of $D$ then has orbits of length 5 and 1 only and . The $\frac{p-1}{5}$ orbits of length 5 form one orbit of $D$ on 5-element subsets. Thus, by Lemma 4, there is only one orbit of on 5-sets with a stabilizer of order 5. Let us assume $\cal D$ to be a $5$-$(p+1,6,1)$ design admitting . Then an orbit $T$ of $U$ of size 5 is contained in exactly one block $B$ of $\cal D$. This block is of size 6 and has to be invariant under $U$. So, $B$ consists of $T$ and an additional fixed point of $U$. We have to choose one of the two fixed points of $U$ to determine the first orbit of PSL(2,p) that has to belong to the design $\cal D$. The two choices lead to isomorphic solutions, since PGL(2,p) maps one of the orbits onto the other one.


We now investigate other orbits of 5-sets and 6-sets.


Theorem 5: Let $p \equiv\ 3\ mod\ 4$ and $T$ a 5-set whose stabilizer in $PSL(2,p)$ has an order different from 5. Then For the block $K$ containing $T$ of a $5$-$(p+1,6,1)$ design admitting $PSL(2,p)$ we have that divides $6$.


Proof. A subgroup $U \ne id$ leaving a 5-set $T$ invariant acts on $T$. No elements of $PGL(2,p)$ different from the identity has more than 2 fixed points. So, the orbits on $T$ must be of type (5), (4,1), (3,2), (3,1,1), (2,2,1). By assumption (5) does not occur. Since 2 does not divide $(p-1)/2$, no element of order 2 of $PSL(2,p)$ has any fixed point. So, (4,1), (2,2,1) do nor occur. By Corollary 3, no element of order 3 fixes $T$. Therefore, $(3,2)$ and $(3,1,1)$ do not occur. So, The stabilizer of a 6-set $K$ then has orbits of length on the 5-sets contained in $K$. So, where $x$ is the number of orbits. $\Diamond$

We conclude that all stabilizers of blocks of a Steiner 5-system $5$-$(p+1,6,1)$ with automorphism group $PSL(2,p)$ must have orders in $\{1,2,3,5,6\}$.



We want to derive some conditions on the numbers of blocks which lie in orbits of a fixed length.

Let $a_i$ be the number of orbits of size $\frac{\vert G\vert}{i}$ of $ G = PSL(2,p)$ on the blocks of the design. Then


\begin{displaymath} b = a_1 \vert G\vert + a_2 \vert G\vert/2 + a_3 \vert G\vert/3 + a_5 \vert G\vert/5 + a_6 \vert G\vert/6. \end{displaymath}

From the general formula for the number of blocks in a $t$-design we obtain in this case


\begin{displaymath} b = {v\choose 5}/6. \end{displaymath}

Then,


has to be inserted into the equation.

After cancelling we obtain



This equation can be reduced modulo some primes to get short relations. Reducing modulo 5 gives our already known result that if 5 divides $\vert PSL(2,p)\vert$ because also .


We consider possibilities of prescribing certain choices of stabilizers. If only one of all $a_i$ is assumed to be non-zero then we obtain the following results.


Theorem 6 Let a $5$-$(p+1,6,1)$ design with automorphism group $PSL(2,p)$ partition into $a$ $3$- $(p+1,6,\lambda)$ designs with automorphism group $PSL(2,p)$ consisting of only one orbit of $PSL(2,p)$ of length $\frac{\vert PSL(2,p)\vert}{i}$ each. Then either $i = 1$ and $p+1 \equiv \ 84, \ 228 \ mod \ 360$ or $i = 2$ and $p+1 equiv \ 48,\ 84 \ mod \ 180$ or $i=5$ and $p = 11$.


Proof. We only have to consider the cases $i \in \{1,2,3,5,6\}$. The case $i = 1$ is already contained in [5]. So let now $i = 2$. Then


We write this as


and reduce modulo 4,5, and 9. Since $v$ is even, 4 divides $v$. We have the solutions $v \equiv 3,\ 4 \ mod\ 5,\ 9$ such that we have four combinations modulo 180 by the Chinese Remainder Theorem. The solutions $p+1\equiv 4\ mod \ 180$ and $p+1\equiv 148\ mod \ 180$ would imply that 3 divides $p$. So, only the claimed cases remain for $i = 2$. There is one further case for $i=5$ where each of the only two existing orbits of 6-sets with a stabilizer of order 5 is already a $5$-$(p+1,6,1)$ design. That is the well known small Witt design with the parameters $5$-$(12,6,1)$. In all other cases the number of orbits of length $\frac{\vert PSL(2,p)\vert}{i}$ needed to form a $5$-$(p+1,6,1)$ design is larger than the existing number of orbits on 6-sets with a stabilizer of order $i$. To get this number of required orbits the number of bocks

\begin{displaymath} b = {v\choose 5}/6 \end{displaymath}

of the 5-design has to be divided by $\frac{\vert PSL(2,p)\vert}{i}$. This number is $\frac{i}{60}(\frac{v}{3}-1)(\frac{v}{2}-2)$. We will show in Theorem 7 that there exist only $\frac{v-12}{12}$ orbits with stabilizer $C_3$ and $\frac{v}{6} +1$ orbits with a stabilizer of order 6. In both cases there are no solutions. $\Diamond$

One can discuss further more complicated cases of selecting several stabilizers with the same methods. We will give some experimental results on existing Steiner systems in such situations below.

next up previous
Next: Subgroups of order up Up: Partitioned Steiner 5-Designs Previous: Introduction
N.N. 2002-02-25

University of Bayreuth -