´

next up previous
Next: Bibliography Up: Partitioned Steiner 5-Designs Previous: Subgroups of order up

Invariants

Each of the stabilizers of order 6 acts transitively on any invariant 6-set $K$. So, there is only one 5-set orbit on $K$. Correspondingly, the column for $K^{PSL(2,p)}$ in the Kramer-Mesner matrix has only one entry 1 and all other entries are 0. So, in these cases, we easily determine the entries of the Kramer-Mesner matrix in these columns. The remaining cases are more complicated. Here we use Alltop's Lemma. That requires for each 5-set $T$ contained in a representative $K$ of a 6-set orbit with stabilizer $U$ to find out the 5-set orbit of $T$. We do this by computing an invariant which separates the 5-set orbits.


If a group acts $t$-transitive then any $t$-element sequence of pairwise different elements can be mapped onto any other such sequence by some group element. If the stabilizer of a sequence $S$ acts trivially then already the sequence of the image points of $S$ determines the image points of all other points.

To see this assume there would be different image points for some element $\omega$. That would mean that there are two group elements $g,h$ such that $S^g = S^h$ but $\omega^g \ne \omega^h$. Then $gh^{-1}$ fixes each element of $S$ and thus should be trivial by assumption. But then $gh^{-1}$ also fixes $\omega$.


Any sequence of pairwise different entries of length bigger than $t$ can be truncated after the first three entries. This is a projection that is compatible with the group action. So, two longer sequences with identical starting sequence $S$ of length $t$ are in the same orbit only if some element in the stabilizer of the first $t$ elements maps one onto the other. If the stabilizer is trivial all these sequences lie in pairwise different orbits. This strategy of using mappings that are compatible with the group action to simplify the problem is called homomorphism principle [14], [16]. We have already used this approach in Lemma 4 where the homomorphism of group actions is the assignment of the stabilizer to its k-set.


If a group is regular on the orbit of $S$ then the orbit of each sequence $T$ with starting subsequence $S$ can be uniquely described by first applying the unique group element $g$ that maps the starting sequence onto $S$ to $T$ and then using the sequence of the images of remaining points under $g$ as an invarant.


A prominent example of this kind is the cross-ratio of geometry. The group $ GL(2,p^f)$ acts 3-transitive on the projective line and regular on 3-sequences of pairwise different 1-dimensional subspaces. By means of linear algebra a matrix can be found mapping one such sequence onto a given second one. In particular, taking as the first sequence a standard representative produces invariants. For any 4-sequence the image of the fourth point after normalizing the first 3-element sequence uniquely determines the orbit.


In any subgroup the stabilizer of three points acts trivially. So, if one first determines each orbit of the subgroup on the 3-sequences and then uses the image of the fourth point one again has an invariant. We use this for $PSL(2,p)$. This group is 2-transitive and the stabilizer of two points is transitive on those points that lie in the same image of the determinant, that is those that are either all squares or all non-squares.


In this way we can map each sequence of 4 pairwise different points onto a unique representative of its orbit. We define some ordering on the set of these representatives and declare the smallest of all representatives from all sequences of 4 pairwise different points of a 5-set $K$ as the representative of $K$.


Of course this could be done as well for any $k$-sets. But for larger $k$ we get too many 4-sets contained in a $k$-set. So, for $k = 6$ and our special goal of finding Steiner systems we here make use of the following observation. If a 6-set is contained in an orbit that already occured then the 5-orbits it covers are already covered by the earlier found representative. In terms of the Kramer-Mesner matrix that would mean that the column computed for the new set is identical to an already existing one. So, we omit multiple columns.


There are cases where 6-sets from different orbits produce identical columns of the Kramer-Mesner matrix. But if we look for Steiner systems we can use at most one of two such columns. So, we could store for each column the multiplicity of its occurrence and then multiply each solution with the factors of all columns belonging to that solution. This would allow to count the complete number of solutions. Then the number of isomorphism types is just half of the number of solutions by [16]. This has not yet been implemented.


We work out the computation. Take $<(1,0)>$ and $<(0,1)>$ as the representatives of the sequences of two 1-dimensional subspaces. Then given any two subspaces $<(1,a)>$ and $<(1,b)>$ or $<(0,1)>$ we can determine a matrix mapping the given sequence onto the sequence of representatives.


The matrix

\begin{displaymath}\left( \begin{array}{cc} 1 & -a\\ 0 & 1 \end{array} \right) \end{displaymath}

maps $(<(1,a)>,<(0,1)>)$ onto $(<(1,0)>,<(0,1)>)$ ,


The matrix

\begin{displaymath}\left( \begin{array}{cc} a & 1\\ -1 & 0 \end{array} \right) \end{displaymath}

maps $(<(0,1)>,<(1,a)>)$ onto $(<(1,0)>,<(0,1)>)$ ,


The matrix

\begin{displaymath}\left( \begin{array}{cc} b(b-a) & -a\\ a-b& 1 \end{array} \right) \end{displaymath}

maps $(<(1,a)>,<(1,b)>)$ onto $(<(1,0)>,<(0,1)>)$ ,


So, in each case we know the matrix $M$ transforming a given sequence of two 1-dimensional subspaces onto the standard basis. We have chosen the matrices so that the determinant $det(M)$ is a square modulo $p$.


The matrix $M$ can be applied to all entries of a 4-sequence such that the first two members are mapped onto $<(1,0)>$ and $<(0,1)>$. So, in a first step, the sequences are normalized in their first two components. This can be done in constant time.


We now consider the second step, where the third component is normalized. The first two components now have to remain unchanged. The subgroup of all matrices fixing the two subspaces $<(1,0)>$ and $<(0,1)>$ consists of the matrices of the form $diag(1,z)$ where $z \ne 0$. There are $p-1$ such matrices. Since any matrix that fixes 3 1-dimensional subspaces must fix all 1-dimensional subspaces, this subgroup acts regularly on the set of subspaces of the form $<(1,a)>$ for $a = 1,\cdots ,p-1$. We chose as a representative $<(1,1)>$. The matrix $diag(1,a^{-1})$ normalizes the third component. So, there is only one orbit on 3-sequences under $PGL(2,p)$.


A sequence

\begin{displaymath}(<(1,a)>,<(1,b)>,<(1,c)>,<(1,d)>)\end{displaymath}

is transformed into normal form by first transforming by

\begin{displaymath}\left( \begin{array}{cc} b(b-a) & -a\\ a-b& 1 \end{array} \right) \end{displaymath}

and then by

\begin{displaymath}\left( \begin{array}{cc} 1 & 0\\ 0 & \frac{(a-b)(c-b)}{c-a} \end{array} \right) \end{displaymath}

So, the product of these transformations

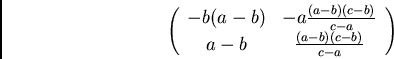
\begin{displaymath}\left( \begin{array}{cc} -b(a-b) & -a\frac{(a-b)(c-b)}{c-a}\\ a-b & \frac{(a-b)(c-b)}{c-a} \end{array} \right) \end{displaymath}

sends $<(1,d)>$ to $<(1,\frac{(a-d)(b-c)}{(b-d)(a-c)})>$.


The quotient

\begin{displaymath}\frac{(d-a)(c-b)}{(d-b)(c-a)}\end{displaymath}

thus is an invariant of the orbit of the given sequence under $PGL(2,p)$. This quotient is known as the cross-ratio in finite geometry.


In case of the special linear group the diagonal matrix has to lie in the coset of a matrix with determinant 1 modulo the kernel of the action of $PGL(2,p)$ on the set of all 1-dimensional subspaces. This kernel consists of all matrices of the form

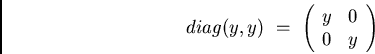
\begin{displaymath}diag(y,y) \ = \ \left( \begin{array}{cc} y & 0\\ 0 & y \end{array} \right) \end{displaymath}

such that their determinant is a square. The squares form a subgroup of index two in the multiplicative group of residues modulo $p$, which therefore has $\frac{p-1}{2}$ elements. So, the $p-1$ subspaces lie in two orbits of length $\frac{p-1}{2}$ each. A representative of the first orbit is $<(1,1)>$ and the orbit consists of all $<(1,z)>$ where $z$ is a square. If 4 divides $p+1$ then 4 does not divide $p-1$. So, the multiplicative group of residues modulo $p$ has no element of order 4 such that there is no $y$ with $y^2 = -1$. We have found the non-square $-1$ which gives rise to a representative $<(1,-1)>$ of the other orbit.


We now have seen that there are two orbits of PSL(2,p) on the set of sequences of length 3 with representatives

\begin{displaymath}(<(1,0)>,<(0,1)>,<(1,1)>)\end{displaymath}

and

\begin{displaymath}(<(1,0)>,<(0,1)>,<(1,-1)>).\end{displaymath}

If we apply the matrix

\begin{displaymath}\left( \begin{array}{cc} 0 & -1\\ 1 & 0 \end{array} \right) \end{displaymath}

of determinant 1 to the first sequence we obtain a permuted version of the second representatives. This shows that the corresponding 3-element sets of 1-dimensional subspaces are in one orbit. This means that $PSL(2,p)$is 3-homogeneous.


For our goal of normalizing a given sequence of 1-dimensional subspaces we, after having transformed the sequence such that the first two components are normalized, have to multiply with some $<(1,z)>$ where $z$ is a square such that we either get $<(1,1)>$ or $<(1,-1)>$ as the third component. The first case is just the cross-ratio derived above. The second one is obtained similarly. It turns out that then $<(1,d)>$ is sent to $<(1,\frac{(d-a)(c-b)}{(d-b)(a-c)})>$. So, in this case we have to multiply the cross-ratio by -1. That allows to use the well known mathematical term of a Legendre symbol. For $p$ a prime and $0<a<p$ one has

\begin{displaymath} \left( \frac{a}{p}\right) \ = \ 1\end{displaymath}

if $a$ is a quadratic residue modulo $p$ and

\begin{displaymath} \left( \frac{a}{p}\right) \ = \ -1\end{displaymath}

if $a$ is a non-quadratic residue modulo $p$. So, if $4\vert p+1$ then the invariant is the product of the cross-ratio and the Legendre symbol.


Using this invariant, the orbit of a 4-sequence can be determined in constant time.


Now we have achieved a sequence of the form

\begin{displaymath} (<(1,0)>,<(0,1)>,<(1,1)>,Y) \end{displaymath}

or

\begin{displaymath} (<(1,0)>,<(0,1)>,<(1,-1)>,Y) \end{displaymath}

where $Y = <(1,y)>$ or $Y = <(0,1)>$. By the homomorphism principle, applied to the projection to the first 3 components, two such sequences could be in the same orbit only if they are mapped one onto the other by some element in the stabilizer of the firest three components. This stabilizer is trivial such that all choices of $Y$ in the two sequences belong to pairwise different orbits. The pair $<(1,1)>,Y$ or $<(1,-1)>,Y$ thus is an invariant for the orbits on sequences of length 4.

Of course, this can be continued to sequences of length 5 and longer.


We now consider 4-element subsets instead of sequences. They can be obtained from the sequences by the fusion version of the homomorphism principle. A given 4-set $T$ can be arranged as a sequence 24 times. So, we will get 24 values of our invariant for $T$. Each transformation also transforms $T$ to some $T'$. The sequences we can form from $T'$ are in the same orbits as the sequences we have formed from $T$. So, we don't have to iterate this process. We can define the set $T'$ coming from the lexicographically smallest sequence among the 24 sequences as the canonical representative. We also can use the transformation which transformed the selected sequence into canonical form for transforming $T$ into canonical form. In fact, if we take the 24 sequences of pairwise different points from $T'$ then by normalizing them we will get back those that we obtained from $T$. This shows that there is a bijection between the set of all 24 values of the invariant and the selected smallest one.


Alltogether we have presented a constant time algorithm which computes for any given 4-element subset the canonical representative of its orbit and a matrix which does this transformation.

A slight variation should be made when many 4-sets have to be transformed into canonical form. Then searching each time for a square $z$ such that

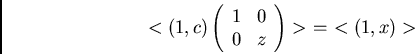
\begin{displaymath}<(1,c) \left( \begin{array}{cc} 1 & 0\\ 0 & z \end{array} \right) > \ = \ <(1,x)> \end{displaymath}

where $x = 1$ or $x=-1$ would take too much time. So, a table can be computed first which contains for each value of $c$ the corresponding square $z$. This can be done in linear time, since either $z$ is the inverse of $c$ and then $c$ is a square or $-z$ is the inverse of $c$ and then $c$ is a non-square. So, besides a table of inverses another table of squares is needed.


The stabilizer of $T'$ is obtained by taking the transforming elements that map one sequence onto another one that also lies in $T'$. The order of the stabilizer is obtained by just the number of transformed sequences that lie in $T'$.


From the orbits on 4-sets we can in a further step get the orbits on 5-sets. If a 5-set $K$ is given, then one can form 5 partitions $K = T \cup \{x\}$ into a sequence of a 4-set $T$ and the remaining element. Transform $K$ by the same element of $PSL(2,p)$ that maps $T$ onto its canonical representative $T'$. Then the stabilizer of $T'$ may map the transformed point $x'$ onto a smaller one. Choose the smallest one to get a representative on the set of all partitions of a 5-set into two components of sizes 4 and 1.


The stabilizer will be trivial in the case where we know in advance that already the stabilizers of all 5-sets are trivial. So, then we need not compute them in this case. We will get 5 different orbits of partitions that fuse to the same 5-set. The smallest of them defines the canonical representative for our 5-set.


The discussion yields the following result.


Definition For a sequence $S$ of 4 pairwise different 1-dimensional subspaces of $V(2,p)$ let the cross-ratio $cr(S)$ of $S$ and the square indicator $si(S)$ of $S$ be defined by the following table.


$S$ $cr(S)$ $si(S)$
$(<(1,a)>,<(1,b)>,<(1,c)>,<(1,d)>)$ $\frac{(a-d)(b-c)}{(a-c)(b-d)}$

1 if $\frac{a-c}{(a-b)(b-c)}$ is a quadratic residue
-1 else
$(<(1,a)>,<(1,b)>,<(1,c)>,<(0,1)>)$ $\frac{(b-c)}{(a-c)}$

1 if $\frac{a-c}{(a-b)(b-c)}$ is a quadratic residue
-1 else
$(<(1,a)>,<(1,b)>,<(0,1)>,<(1,d)>)$ $\frac{(a-d)}{(b-d)}$

1 if $a-b$ is a quadratic residue
-1 else
$(<(1,a)>,<(0,1)>,<(1,c)>,<(1,d)>)$ $\frac{(a-d)}{(a-c)}$

1 if $c-a$ is a quadratic residue
-1 else
$(<(0,1)>,<(1,b)>,<(1,c)>,<(1,d)>)$ $\frac{(b-c)}{(b-d)}$

1 if $b-c$ is a quadratic residue
-1 else


Theorem Let $S$ be a sequence of 4 pairwise different 1-dimensional subspaces of $V(2,p)$. Then the orbit of $S$ under $GL(2,p)$ is uniquely determined by $cr(S)$. The sequence $S$ is transformed into normal form

\begin{displaymath}(<(1,0)>,<(0,1)>,<(1,1)>,<(1,cr(S))>)\end{displaymath}

by the matrix

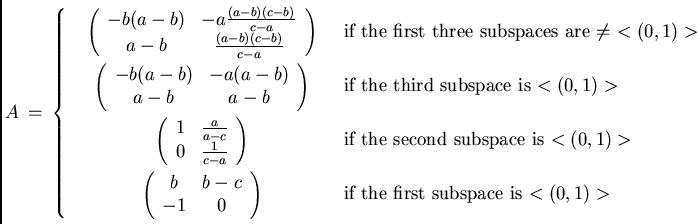
\begin{displaymath} A \ = \ \left\{ \begin{minipage}{16cm} \begin{minipage}{6cm}... ...ge}if the first subspace is $<(0,1)>\\ \end{minipage}\right. \end{displaymath}

If 4 divides $p+1$ then the orbit of $S$ under $SL(2,p)$ is uniquely determined by $cr(S)$ and $si(S)$. The sequence $S$ is transformed into normal form

\begin{displaymath}(<(1,0)>,<(0,1)>,<(1,si(S))>,<(1,si(S)\cdot cr(S))>)\end{displaymath}

by the matrix

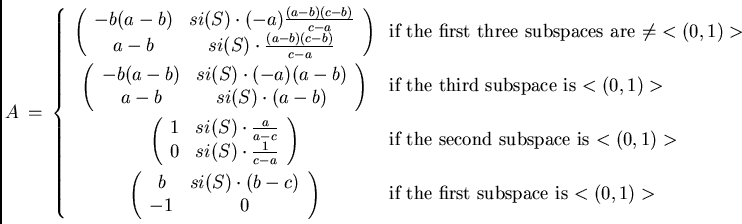
\begin{displaymath} A \ = \ \left\{ \begin{minipage}{16cm} \begin{minipage}{7cm}... ...ge}if the first subspace is $<(0,1)>\\ \end{minipage}\right. \end{displaymath}


Using these formulae the time complexity of determining the orbit of a 4-element sequence of pairwise different 1-dimensional subspaces is dominated by forming a constant number of arithmetic operations and deciding whether some number is a quadratic residue modulo $p$. The last problem can be solved in time $O(log(p))$ using the Gauß reciprocity formula, [19], by a strategy similar to Euclid's gcd algorithm.

For a small prime $p$ and many tasks of computing canonical forms it is a better strategy to first set up tables of squares and of inverses in linear time and then for each canonical form computation using only constant time.



.


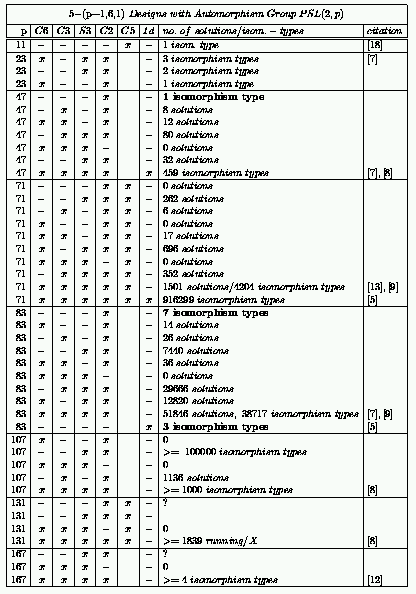
Remarks


The next open case is $PSL(2,191)$. For prime powers there are further results. There exist at least $303$ isomorphism types of $5$-$(244,6,1)$ designs with automorphism group $P\Sigma L(2,3^5)$ [5].


Besides that there exists one $5$-$(36,6,1)$ design with automorphism group $C_2 \times PGL(2,17)$.


Most remarkable are the partitionable Steiner systems consisting of orbits of the same size. We have obtained exactly 1 isomorphism type for a prescribed stabilizer $C_2$ and $p = 47$ and exactly 7 isomorphism types for $p = 83$.


The next case would be v = 228:


We would need 280 orbits with stabilizer $C_2$ or 140 orbits with trivial stabilizer for a $5$-$(228,6,1)$ design. So, we need only half as many orbits if we prescribe a trivial stabilizer as we need with stabilizer $C_2$. But there are by far too many orbits with trivial stabilizer to choose the 140 orbits from. So, it might be easier to prescribe $C_2$.


The total number of $PSL(2,227)$ orbits on 6-sets is 32300. Out of these only 2070 have length $\frac{\vert PSL(2,p)\vert}{2}$. The number of 5-orbits is 840. In the Kramer-Mesner Matrix, reduced to these 6-orbits, in each column there are exactly 3 entries 1 and all others are 0.


The effect of the space reduction by using only a sparse matrix can be seen with $PSL(2,443)$ where prescribing stabilizer $C_2$ results in a matrix of 3234 5-orbits by 8028 6-orbits. The full matrix requires 52 MB while the sparse matrix only needs 0.53 MB. This problem size is far out of our present reach.


next up previous
Next: Bibliography Up: Partitioned Steiner 5-Designs Previous: Subgroups of order up
N.N. 2002-02-25

University of Bayreuth -