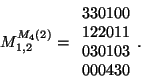The q-analog of the Kramer-Mesner matrix

The next step in the construction is the evaluation of the entries of the Kramer-Mesner matrices. We achieve this goal by using the information obtained during the ladder game.

We can restrict attention to Kramer-Mesner matrices , because of

$\begin{displaymath}M_{t}\cdot M_{k} = \left\vert\left[ k-t\atop k-t'\right]_q\right\vert\cdot M_{k}.\end{displaymath}$

(The analogous equation -- with binomial coefficients instead of the Gaussian numbers -- holds for designs on sets, the proof of it is easily generalized to the -analog.

The matrix can be obtained as follows: We assume the representatives of the double cosets of and $GL_v(q)_{S_{t}}$ , representatives of the double cosets of and $GL_v(q)_{S_t}$ and the corresponding orbit graph. Now the entry of $M_{$ indexed by the orbits

$\begin{displaymath}\varphi^{-1}_t(A\Phi GL_v(q)_{S_t})\in A{\backslash\!\!\backs... ...{t}})\in A{\backslash\!\!\backslash}\left[v\atop t\right]_q\end{displaymath}$

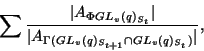
$\begin{displaymath}\sum\frac {\vert A_{\Phi GL_v(q)_{S_t}}\vert}{\vert A_{\Gamma (GL_v(q)_{S_{t}}\cap GL_v(q)_{S_t})}\vert},\end{displaymath}$

where the sum is over all double cosets $A\Gamma(GL_v(q)_{S_{t}}\cap GL_v(q)_{S_t})$ which are connected with the double coset $A\Psi GL_v(q)_{S_{t}}$ and which are connected with the double coset $A\Phi GL_v(q)_{S_t}$ at the same time.

If we take our last example then we get the Kramer-Mesner matrix:

$M_{1,2}^{M_4(2)}$	(3,0,4)	(3,1,2,)	(3,2,6)	(3,3,6)	(3,4,8)	(3,5,4)
(5,0,6)	6/2	6/2	0	6/6	0	0
(5,1,4)	4/4	4/2	4/2	0	4/4	4/4
(5,2,6)	0	6/2	0	6/6	0	6/2
(5,3,24)	0	0	0	24/6	24/8	0

and thus the -analog of the Kramer-Mesner matrix turns out to be

$\begin{displaymath} M_{1,2}^{M_4(2)}= \begin{array}{c} 3 3 0 1 0 0\\ 1 2 2 0 1 1\\ 0 3 0 1 0 3\\ 0 0 0 4 3 0\\ \end{array}. \end{displaymath}$

Back to the title page