The ladder game
|
The ladder game is an algorithm for the stepwise determination of transversals
of the sets of double cosets ![]() to
to ![]() for a subgroup
for a subgroup ![]() of a group
of a group ![]() and a sequence of subgroups, a
so-called ladder,
and a sequence of subgroups, a
so-called ladder, ![]() of
of ![]() with either
with either ![]() or
or ![]() for all
for all ![]() .
.
We call a step from ![]() to
to ![]() with
with ![]() a step down. A double coset of
a step down. A double coset of ![]() and
and ![]() splits into double cosets of
splits into double cosets of ![]() and
and ![]() :
:
![]()
for a
transversal ![]() of
of ![]() . Therefore, a transversal of the
. Therefore, a transversal of the ![]() -double cosets is a subset of
-double cosets is a subset of ![]() where
where ![]() means a transversal of the
means a transversal of the ![]() -double
cosets. This subset has to be determined.
-double
cosets. This subset has to be determined.
A step up from ![]() to
to ![]() is a step with
is a step with ![]() . Such double cosets of
. Such double cosets of ![]() and
and ![]() fuse to a double coset of
fuse to a double coset of ![]() and
and ![]() :
:
![]()
for a
transversal ![]() of
of ![]() . We obtain a transversal of the double cosets of
. We obtain a transversal of the double cosets of ![]() and
and ![]() as a subset of a transversal of the
double cosets of
as a subset of a transversal of the
double cosets of ![]() and
and ![]() .
.
To keep down the complexity
of this algorithm, we should try to choose a ladder ![]() with a small index between
with a small index between ![]() and
and ![]() for all
for all ![]() , because during each step, dow or up,
respectively, we run through a transversal of
, because during each step, dow or up,
respectively, we run through a transversal of ![]() and
and ![]() , respectively.
, respectively.
In order to visualize the
ladder game we introduce a graph which we call orbit graph:
- The
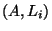 -double cosets,
-double cosets, 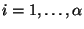 , correspond to the vertices of the graph.
, correspond to the vertices of the graph. - Two vertices are connected by an edge iff
the corresponding double cosets
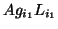 and
and 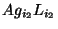 fulfill
fulfill 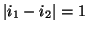
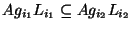 or
or 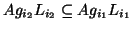 .
. - Each vertex is labeled by a tuple
 , where
, where 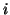 means the step in the ladder
game,
means the step in the ladder
game, 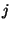 is the
is the 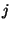 -th double coset of
-th double coset of 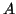 and
and 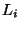 and
and 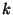 is the order of
the stabilizer of the corresponding double coset in
is the order of
the stabilizer of the corresponding double coset in 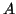 .
.
Let us
return to the determination of transversals of ![]() and of
and of ![]() We need a ladder of
We need a ladder of ![]() containing
containing
![]() and
and ![]() . For this purpose we take the following sequence of parabolic subgroups
(generalizing this way the ladder game that we applied to designs on sets,
where we took a ladder of Young subgroups!)
. For this purpose we take the following sequence of parabolic subgroups
(generalizing this way the ladder game that we applied to designs on sets,
where we took a ladder of Young subgroups!)
$$
![]()
$$
![]()
$$
![]()
$$
![]()
![]()
$$
![]()
$$
![]()
$$
![]()
as a
ladder. Starting from the trivial transversal of ![]() we can determine step by step all transversals
of
we can determine step by step all transversals
of ![]() for all
for all ![]() .
.
Let us display a concrete
example: We take the parameters ![]() and, for
and, for ![]() we
choose
we
choose ![]() , the complete monomial group, which is isomorph to the wreath product
, the complete monomial group, which is isomorph to the wreath product ![]() . Then we get the following orbit graph:
. Then we get the following orbit graph:
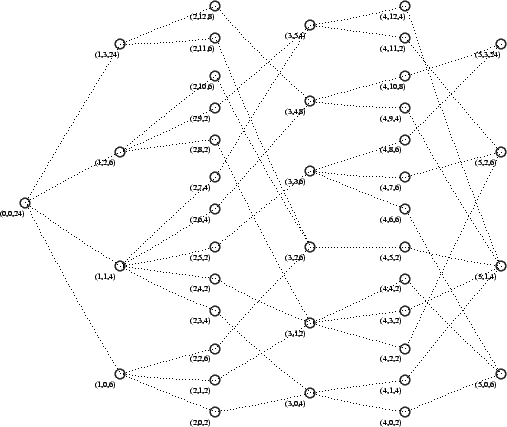
In this
graph the vertices with the labels ![]() correspond to the orbits of
correspond to the orbits of ![]() on the
set of
on the
set of ![]() -supspaces
of
-supspaces
of ![]() and the vertices labeled by the tuples
and the vertices labeled by the tuples ![]() correspond to the orbits of
correspond to the orbits of ![]() on the
set of
on the
set of ![]() -subspaces.
-subspaces.