Prescribing a group of automorphisms

The intention is to reduce the incidence matrix to a much smaller matrix so that we can solve the corresponding diophantine system of equations by running a modern implementation of the LLL-algorithm on a workstation or a personal computer. To achieve this goal we use the concept of finite group actions and the prescription of a group of automorphisms (similar to the methods we use in the above mentioned research project on the construction of classical $t-(v,k,\lambda)$ -designs). Of course, this prescription is risky since there may be no designs with that particular group of automorphisms, but if there are such designs then it will pay since the number of rows of the incidence matrix, which is the number of -subspaces in , will reduce to the number of orbits of that group, and the same holds for the number of columns. This will bring the construction problem within reach of computers!

An automorphism of a $t-(v,k,\lambda;q)$ -design ${\cal{B}}$ is an element $\Phi$ of the general linear group which leaves the design invariant, i. e. it maps blocks onto blocks, it permutes the design:

$\begin{displaymath}\{\Phi(K)\mid K\in {\cal{B}}\}={\cal{B}}.\end{displaymath}$

A group consisting only of automorphisms of $\cal B$ is an automorphism group of ${\cal{B}}$ , the maximal group with this property is called the (full) automorphism group of ${\cal{B}}.$ The crucial facts are now as simple as this:

2.1 Remarks If $A\leq\ GL_v(q)$ is an automorphism group of the $t-(v,k,\lambda;q)$ -design ${\cal{B}},$ then

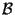${\cal{B}}$ consists of full orbits of 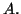We may therefore restrict our attention to the orbits of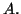
The inclusion 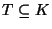$T\subseteq K$ of 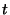-spaces 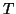in 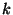-spaces 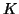is invariant under the action of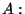

$\begin{displaymath}\Phi(T)\subseteq\Phi(K). \end{displaymath}$

Therefore, for $T\in\left[ v \atop t \right]_q$ and $K\in\left[ v \atop k \right]_q,$ the number of 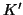in the orbit of 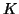which lie above 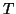is constant on the orbit of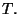
This number is a sum of values of the 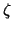$\zeta$ -function on the lattice of subspaces of 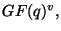and we shall denote it as follows:

$\begin{displaymath} \widetilde{\zeta}(T,K):=\sum_{K'\in A(K)}\zeta(T,K')=\vert\{K'\mid K'\in A(K),T\subseteq K'\}\vert.\end{displaymath}$

$\Box$

This embeds this problem into the theory of group actions on posets (cf. [8]) and it motivates the introduction of the matrix , a -analog of the Kramer-Mesner matrix ([10]) for standard combinatorial designs on sets. Its rows (resp. columns) are indicated by the elements (resp. ) of a transversal of the set $A{\backslash\!\!\backslash}\left[ v \atop t \right]_q$ of orbits of on $\left[ v \atop t \right]_q$ (resp. of a transversal of the set $A{\backslash\!\!\backslash}\left[ v \atop k \right]_q$ of orbits of on $\left[ v \atop k \right]_q$ ), and the entries are the above mentioned values $\widetilde{\zeta}(T,K):$

$\begin{displaymath} M^A_{t,k}:=(m^A_{T,K}),\ \mbox{where}\ m^A_{T,K}:=\widetilde{\zeta}(T,K).\end{displaymath}$

The following theorem is now immediate from the above remarks:

2.2 Theorem The set of $t-(v,k,\lambda;q)$ -designs ${\cal{B}}$ having $A\le GL_v(q)$ as an automorphism group can be obtained from the 0-1-vectors solving the linear system of equations

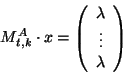
$\begin{displaymath}M_{t,k}^A\cdot x = \left(\begin{array}{c} \lambda\\ \vdots\\ \lambda \end{array} \right)\end{displaymath}$

in the following way:

$\begin{displaymath}{\cal{B}}:=\bigcup_{K\colon x_K=1}A(K). \end{displaymath}$

$\Box$

This method of generalizing the Kramer-Mesner approach to -analogs of designs was already used in [7], but the derivation of 2-designs which admit which is given there, uses ad hoc methods which cannot be used in the general case. We are therefore going to describe now a general approach that can be used, in principle, in any case. The first step in this direction is the evaluation of transversals of the sets of orbits

$\begin{displaymath}A{\backslash\!\!\backslash}\left[ v \atop t \right]_q\ \mbox{and}\ A{\backslash\!\!\backslash}\left[ v \atop k \right]_q. \end{displaymath}$

For this purpose we can use the Fundamental Lemma of the theory of finite group actions (see e. g. [8],[11]) which reads as follows:

2.3 The Fundamental Lemma If

$\begin{displaymath}G\times X\to X\colon(g,x)\mapsto gx \end{displaymath}$

denotes a finite group action, and a subgroup of then, for each $x\in X,$ the set of orbits of on can be mapped bijectively onto the set of -double cosets:

$\begin{displaymath}U{\backslash\!\!\backslash}G(x)\to U\backslash G/G_x=\{UgG_x\mid g\in G\}\colon U(gx)\mapsto UgG_x, \end{displaymath}$

where means the stabilizer of in $\Box$

In order to apply it we use the fact that the general linear group is transitive both on $\left[ v \atop t \right]_q$ and on $\left[ v \atop k \right]_q,$ and so the following is true:

2.4 Corollary We can obtain the desired transversals of the orbit sets of from transversals of sets of double cosets by reverting the following bijections

$\begin{displaymath}\varphi_t:A{\backslash\!\!\backslash}\left[ v \atop t \right]... ...lash GL_v(q)/GL_v(q)_T\colon A(\Phi(T))\mapsto A\Phi GL_v(q)_T \end{displaymath}$

and

$\begin{displaymath}\varphi_k:A{\backslash\!\!\backslash}\left[ v \atop k \right]... ...sh GL_v(q)/ GL_v(q)_K\colon A(\Phi(K))\mapsto A\Phi GL_v(q)_K ,\end{displaymath}$

where and are (arbitrary but fixed) elements of $\left[ v \atop t \right]_q,$ $\left[ v \atop k \right]_q,$ respectively, while and denote their stabilizers in the full linear group. $\Box$

For and , respectively, we can take the subspaces generatedby the , respectively first unit vectors, and The corresponding stabilizers $GL_v(q)_{S_t}$ and $GL_v(q)_{S_k}$ consist of the nonsingular matrices with a box of zeros of size $(v-t)\times t$ and $(v-k)\times k$ in the lower left hand corner.

All what remains is the determination of transversals of the sets of double cosets $A\backslash GL_v(q)/GL_v(q)_{S_t}$ and $A\backslash GL_v(q)/GL_v(q)_{S_k}$ . For this purpose we use a generalization of the ladder game introduced by B. Schmalz in [14],[15],[16] in order to construct designs on sets.

Back to the title page