´

Introduction


A $t-(v,k,\lambda)$-design is a set $\cal B$of blocks of order $k$on a set of $v$vertices such that each $t$-subset of the set of vertices is contained in exactly $\lambda$blocks. More formally, let $v:=\{0,\ldots,v-1\}$denote the set of vertices and indicate by

\begin{displaymath} {v\choose k}:=\{K\subseteq v\mid\vert K\vert=k\} \end{displaymath}


the set of $k$-subsets of the set $v$of vertices. Then $\cal B$has to fulfill the following conditions in order to be a $t-(v,k,\lambda)$-design:

\begin{displaymath} {\cal{B}}\subseteq {v\choose k},\ \mbox{and}\ \forall\ T\in ... ...\colon \ \vert\{K\in{\cal{B}}\mid T\subseteq K\}\vert=\lambda. \end{displaymath}


The introduction of a $q$-analog is now obvious: A $t-(v,k,\lambda;q)$-design is a set $\cal B$of subspaces of dimension $k$of $GF(q)^v$such that each subspace of dimension $t$is contained in exactly $\lambda$blocks. More formally, let

\begin{displaymath} \left[ v \atop k \right]_q:=\{K\leq GF(q)^v\mid\ dim(K)=k\} \end{displaymath}


indicate the set of $k$-subspaces of $GF(q)^v.$Then $\cal B$has to fulfill the following conditions in order to be a $t-(v,k,\lambda;q)$-design:

\begin{displaymath} {\cal{B}}\subseteq \left[ v \atop k \right]_q,\ \mbox{and}\ ... ...\colon \ \vert\{K\in{\cal{B}}\mid T\subseteq K\}\vert=\lambda. \end{displaymath}


As $t-(v,k,\lambda;q)$-designs are suitable selections of blocks, they can be described with the aid of the incidence matrix $M^v_{t,k},$the rows of which correspond to the $T\in\left[ v \atop t \right]_q$and the columns of which correspond to the $K\in \left[ v \atop k \right]_q.$The entries $m_{^{v,q}$of $M^{v,q}_{t,k}$are defined as follows:

\begin{displaymath}m_{TK}^{v,q}:=\cases{1,&if $T\subseteq K,$\cr 0,&otherwise.} \end{displaymath}


Hence a $t-(v,k,\lambda;q)$-design ${\cal B}$is nothing but a selection of columns of that particular matrix, or, equivalently, a 0-1-vector $x$which solves the system of linear equations with this particular matrix as matrix of coefficients:

1.1 Corollary   The set of $t-(v,k,\lambda;q)$-designs on $GF(q)^v$is the set of selections of $k$-subspaces that can be obtained from the 0-1-solutions $x$of the sytem of linear equations

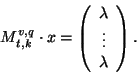
\begin{displaymath} M^{v,q}_{t,k}\cdot x=\left(\begin{array}{c} \lambda\\ \vdots\\ \lambda \end{array} \right). \end{displaymath}


The set $\cal B$of blocks $K$of the design corresponding to the solution $x$is

\begin{displaymath}{\cal B}:=\Bigl\{K\in\left[ v \atop k \right]_q\ \Bigl\vert\ x_K=1\Bigr\}.\end{displaymath}


There are, of course, several trivial cases, where solutions exist, for example

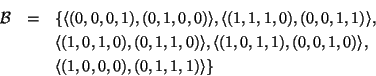
\begin{eqnarray*} {\cal{B}}&=&\{ \langle(0,0,0,1),(0,1,0,0)\rangle,\langle(1,1,1... ...,1,1),(0,0,1,0)\rangle,\\ &&\langle(1,0,0,0),(0,1,1,1)\rangle\} \end{eqnarray*}



is a $1-(4,2,1;2)$design, but we are looking for nontrivial designs. The first examples were presented by S. Thomas ([18]) who found $2-(v,3,7;2)$-designs, for all $v\equiv\pm 1\mbox{ mod }6$. H. Suzuki ([17]) extended this family to families of $2-(v,3,q^2+q+1,q)$-designs for arbitrary prime powers $q$under the same restriction on $v$as above. As far as we know, no nontrivial $t-(v,k,\lambda;q)$-designs have been found yet for $t>2$.

Thomas and Suzuki used geometric arguments for their constructions, but we are interested here in a general approach that allows a systematic and complete construction of such designs (for small parameters), and therefore it has to be implemented on computers. The above lemma opens such an approach but we note that the matrix $M^v_{t,k}$is a very big matrix, so that there is not much hope to find such solutions via solving this big system of diophantine equations.

Back to the title page

University of Bayreuth -