Group selection -
Choose prescribed automorphism group
If you choose the "group" button in DISCRETA you have different possibilities for
further choices. You get the following list:

Here you have to press "Choose prescribed automorphism group" to receive a
list of groups we have implemented. A new window will open:

Besides the possibility of typing in a set of generating permutations by hand
(an example is given) you have the choice between 5 kinds of groups:
|
The first selection is "well known". Here you can choose the symmetric, the
alternating, dieder or the cyclic group on n points (you have to choose the
parameter n first), as well as the holomorph of the cyclic group on n points,
the trivial group, the (only) subgroup of Hol(Cn) of index m or
finally the wreath product of Sn and Sm.
|

|
|
For the construction of designs very useful are the linear groups - you have to
press "linear": we consider
the following matrix groups in their permutation representation. First of all
there is the general linear group GL(n,q) - where q is the order of the
corresponding field - of regular n /times n-matrices; then SL(n,q) is the
special linear group of matrices with determinante 1.
Derived from them we have
the GGL(n,q) where GG stands for Gamma, and the SSl(n,q) where SS stands for
Sigma. The corresponding projective groups we get as factor groups modulo the
center. Then we have the affine groups of affine transformations. Finally, you
can choose the group of affine translations T(n,q), the projective special
unitary group PSU(3,q2) and the Sz(q).
For all groups you have to
choose the parameters n and q.
|

|
You also can use several sporadic groups:
The Mathieu groups M11, M12, M23 and
M24 are simple groups. They are the only nontrivial, at least
4-transitive groups:
- M11: sharply 4-transitive of degree 11, order: 11 · 10
· 9 · 8
- M12: sharply 5-transitive of degree 12, order: 12 · 11
· 10 · 9 · 8
- M23: 4-transitive of degree 23, order: 23 · 22 · 21
· 20 · 3 · 24
- M24: 5-transitive of degree 24, order: 24 · 23 · 22
· 21 · 20 · 3 · 24
The Higman-Sims group HS can be described as the automorphism group of a
combinatorial geometry consisting of a set M of 176 points and a set Q of 176
quadrics. It is 2-transitive in its action on M and has an equivalent
20transitive action on Q. The order of HS is 44.352.000.
|
|
|
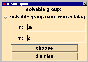
There exists a catalogue of all solvable groups of degree at most 127. With the
parameter n you choose the degree and the choice of m gives you the m-th group
of degree n in the catalogue.
|
|
|
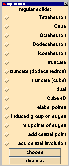
Here you can choose the symmetry groups of regular and semiregular solids.
You start with the choice of one of the platonic solids: tetrahedron, cube,
octahedron, icosahedron and dodecahedron.
Then it is possible to modify the
chosen solid for example by
- truncating the edges (only for vizualizing
the solid the distinction between dodecahedron, cube and the others is
important - the group just the same, namely the induced group of the first
solid),
- considering the dual solid i.e. taking the center of the faces as the
new vertices (the platonic solids are pairwise dual: cube
and octahedron, icosa- and dodecahedron, tetrahedron with itself); it is very
interesting to build the dual of semiregular and archimedian solids,
- taking
the midpoints of edges as the vertices of the new solid and
- adding a central point of a solid; that means adding a fixpoint of
the automorphism group.
In addition you can choose the group of the hypercube (4-dimensional cube).
All those solids are drawn as 3D-graphs. The pictures can be shown on the screen
by pressing the button "group" and "show solid" (examples).
|
|
|
Very useful are the combinations of the different groups. You have 2
possibilities:
- You can choose two groups and combine them by
- appending the second to the first
- building the direct sum
- building the direct product
- building the wreath product
- exponentiation of the first group by the second one
- considering the action on mappings nm
- You can choose one group and
- add a fixpoint
- build a point stabilizer
- induce the action of the group on 2-sets
- induce the action of the group on 2-tuples
- induce the action of the group on the injective 2-tuples
- induce the action of the group on 3-sets
- build the i-th power of the group (you have to type in i)
One example (starting point is the tetrahedron) is given by the following selection:

The resulting designs and details of the construction you can find at this page.
Remark: You have to click on the pictures to get them largely.
Back to the
description .
Back to the
DISCRETA homepage .
Last updated: August 24, 1999, Evi Haberberger







