The schoolgirl problem of Reverend Kirkman (1806-1895)
| "Fifteen young ladies in a school walk out three abreast for seven days in succession; it is required to arrange them daily, so that no two will walk twice abreast." |
This question, posed by Reverend Kirkman in the middle of the previous century, has stimulated mathematics for a long time and finally led to the development of the concept of a design. In mathematical language, we look for a design on 15 points with block length 3, such that every pair of points is contained in at most one block - in fact, it turns out that (15 \choose 2) = 7 · 5 · (3 \choose 2), so every pair of points is contained in exactly one block.
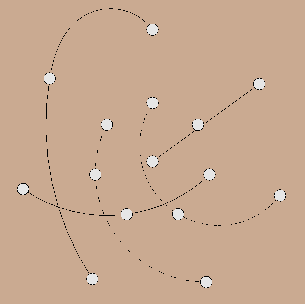
One solution of the problem is given by the following picture:

The following table gives one of the possible solutions you can find within the picture. The suggested numbering of the points is the following: consider the outer circle; the point at the top is labelled 1, then the other points of the outer circle are labelled counterclockwise from 2 to 7. The same procedure labels the points of the inner circle with 8, ..., 14; finally, the central point is labelled 15.

Monday's constellation consists of 5 different kinds of lines in the picture covering all points (i.e. ladies). The constellations of the other days we receive by rotating this constellation counterclockwise each day by one step.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
In mathematical language we have a 2-(15, 3, 1) design: our pointset is V = {1, ..., 15} and we consider blocks of length 3 (there are 5 · 7 = 35 blocks). The important property of these blocks is that each pair of points - we have (15 \choose 2) = 105 of them - is contained in exactly lambda = 1 block.
Another interesting fact is the property, that the 5 blocks forming the constellation for one day give a partition of the 15 points. That's fairly good for the ladies!
Back to the
DISCRETA homepage
last updated: August 31, 1999, Evi Haberberger